|
|
Developmental Biology - Organ Transplants
Predicting The Ideal Transplant Donor & Recipient
It may now be possible to predict the best candidate for receiving an organ transplant...
How to predict the best candidate for receiving an organ transplant; know whether clients of a donor bank will return the loans they request; make the best decisions that coincide with the interests of consumers and perhaps even select someone's ideal donor partner — is a critical need.
Mathematical algorithms constantly analyse millions of items of information like these in order to identify patterns and make predictions in all areas of life. But, in most cases such results give little more than a close prediction that cannot be interpreted and is often affected by biases in the original data.
Now, a team from the research group SEES:lab of the Department of Chemical Engineering of the Universitat Rovira I Virgili (URV) and ICREA has made a breakthrough with development of a new algorithm that makes more accurate predictions while generating mathematical models that also make it possible to more easily understand these predictions.
The results of this research have just been published in the journal Science Advances.
"The aim of our study was to create what is known as a scientific robot, an algorithm that can apply knowledge and the expertise to interpret data."
Marta Sales-Pardo PhD, Associate Professor, Department of Chemical Engineering, Universitat Rovira i Virgili, Catalonia, Spain; and author on the paper.
The algorithm's strength is that it can interprete other theories. Explains Roger Guimerà, an ICREA researcher from the same group: "The algorithm gives you the mathematical relations between variables it has analysed and does it completely independently."
When a company has an enormous amount of data that it wants to exploit, it employs someone to try out various math models and then propose which works best on that data following experimentation. This involves a considerable investment in time and money.
The algorithm developed at the URV blends the best of the two: it processes data automatically, quickly and reliably, as a machine learning system; then it produces an interpretable model.
Another possibility is to find a specialist in machine learning to identify complex patterns in enormous data sets, learn automatically and produce a "black-box" model that makes predictions. However, such systems provide no other information. If the prediction fails it is impossible to know where the error lies and how to prevent a repeat.
The algorithm can be used to analyse and interpret data from any discipline in a process that is much more agile and efficient than those in existence to date. But, the real added value is the information that the system provides.
"In medicine, for example, if you have to take a decision based on data it is very important to understand why each decision has been taken and the risk of making a mistake. Although the algorithm has also shown that it is highly accurate, the most important thing is that you can understand the results because you have built a machine scientist that, with no previous knowledge, can take a set of data and develop a theory that solves the problem posed."
Ignasi Reichardt PhD,
Physicist, SEES, Department of Chemical Engineering, Universitat Rovira i Virgili, Catalonia, Spain.
In this study, the algorithm was applied to a fundamental problem of fluid physics collaborating with the research group Experimentation, Computation and Modelling in Fluid Mechanics and Turbulence of the URV's Department of Mechanical Engineering.
Abstract
Closed-form, interpretable mathematical models have been instrumental for advancing our understanding of the world; with the data revolution, we may now be in a position to uncover new such models for many systems from physics to the social sciences. However, to deal with increasing amounts of data, we need “machine scientists” that are able to extract these models automatically from data. Here, we introduce a Bayesian machine scientist, which establishes the plausibility of models using explicit approximations to the exact marginal posterior over models and establishes its prior expectations about models by learning from a large empirical corpus of mathematical expressions. It explores the space of models using Markov chain Monte Carlo. We show that this approach uncovers accurate models for synthetic and real data and provides out-of-sample predictions that are more accurate than those of existing approaches and of other nonparametric methods.
Authors
Roger Guimerà, Ignasi Reichardt, Antoni Aguilar-Mogas, Francesco A. Massucci, Manuel Miranda, Jordi Pallarès and Marta Sales-Pardo.
Acknowledgments
The authors thank E. G. Altmann, L. A. N. Amaral, A. Arenas, J. Bonet Avalos, and D. Shasha for helpful comments and suggestions. We thank I. Arnaldo for help with the EFS software. We thank A. Arenas for pointing us toward the Nikuradse dataset. We thank M. De Domenico and A. Arenas for sharing the financial success dataset. We thank E. Bazellières and X. Trepat for sharing the cell adhesion dataset. Funding: This project has received funding from the Spanish Ministerio de Economia y Competitividad (FIS2015-71563-ERC, FIS2016-78904-C3-P-1, and DPI2016-75791-C2-1-P). F.A.M. acknowledges financial support by the Spanish MINECO grant PTQ-14-06718 (2016-2019) of the Torres Quevedo Programme. Author contributions: R.G. conceived the research. R.G., I.R., A.A.-M., F.A.M., M.M., and M.S.-P. contributed methods, wrote code for the computational experiments, and carried out computational experiments. All authors designed the computational experiments and interpreted the results, and wrote and edited the manuscript. Competing interests: The authors declare that they have no competing interests. Data and materials availability: A Python implementation of the Bayesian machine scientist and all data needed to evaluate the conclusions in the paper are publicly available from Bitbucket at https://bitbucket.org/rguimera/machine-scientist. Additional data related to this paper may be requested from the authors.
Copyright © 2020 The Authors, some rights reserved; exclusive licensee American Association for the Advancement of Science. No claim to original U.S. Government Works. Distributed under a Creative Commons Attribution NonCommercial License 4.0 (CC BY-NC).
Return to top of page.
| |
|
Feb 10 2020 Fetal Timeline Maternal Timeline News
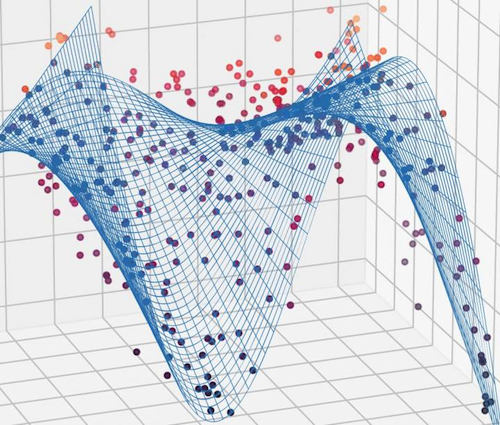 From data (points) given to the scientific robot, it is able to find the law that best describes candidates (blue surface) and their exact mathematical match.
CREDIT URV
|



