|
|
Developmental Biology - Cell Changes
Environmental Noise Changes Cell Structures
Environmental noise appears to affect the cooperation between components that make up cells...
Cells are massive factories, containing a multitude of substations devoted to specific tasks. All are devoted to keeping the organism alive. Until now, researchers have questioned how such diverse components evolve in tandem - especially as each component could evolve in a variety of ways.
Two researchers based in Tokyo, Japan, have developed a statistical physics model to demonstrate how such evolution is possible. The results were published on May 26 in Physical Review Letters.
Their work is based on the idea that the evolutionary potential for each cell component is considered highly dimensional. However, the function of each component actually evolves to make the cell as a whole the most fit, where each piece can be affected by another piece as a result of evolution - that is low dimensionality.
"How can such complex systems adapt to environment yet evolve control with such large degrees of freedom? Recent experiments suggest that physical changes due to adaptation and evolution are highly constrained in a low-dimensional subspace. How does such a drastic dimension reduction emerge?"
Ayaka Sakata PhD, Associate Professor, Institute of Statistical Mathematics.
Sakata and co-author Kunihiko Kaneko, professor of theoretical biology, University of Tokyo, used a spin-glass model to understand how each piece of the puzzle evolves individually to improve the system as a whole.
Their model is based on how an organized system - where the system repeats itself in a stable fashion - can transition into a disorganized system - where connections are stable but random as materials change from non-magnetic to magnetic.
Spins, an intrinsic property of electrons, become aligned under specific conditions. This phenomenon can be mapped in biology, through the activity of genes.
"By forming the problem in the terms of statistical physics, a spin-glass model, we demonstrate how dimensional reduction emerges through the robust response to noise."
Ayaka Sakata PhD, Associate Professor, Department of Statistical Inference & Mathematics, Institute of Statistical Mathematics, Tachikawa, Tokyo, Japan.
Noise is an unpredictable variation in the environment that can cause change in cellular components.
Computer simulations of evolution under high noise led to random, disorganized change — while low noise led to too much variability in components.
Evolution under a moderate level of noise led to low dimensionality when the variety of components was restricted. This characteristic is considered a result of robust evolution to noise level.
"Although the present statistical physics model is highly simplified, it gives a theoretical basis for dimension reduction in biological systems, in which robustness to noise is also essential. In fact, the present model can be interpreted as the evolution of protein to have that function."
Ayaka Sakata.
Abstract
The evolution of high-dimensional phenotypes is investigated using a statistical physics model consisting of interacting spins, in which phenotypes, genotypes, and environments are represented by spin configurations, interaction matrices, and external fields, respectively. We found that phenotypic changes upon diverse environmental change and genetic variation are highly correlated across all spins, consistent with recent experimental observations of biological systems. The dimension reduction in phenotypic changes is shown to be a result of the evolution of the robustness to thermal noise, achieved at the replica symmetric phase.
Authors
Ayaka Sakata PhD, Department of Statistical Inference & Mathematics, Institute of Statistical Mathematics, Tachikawa, Tokyo, Japan; and Kunihiko Kaneko PhD, Meguro-ku, Tokyo, Japan.
Acknowledgements
This work was supported in part by the Japanese Society for the Promotion of Science and the Ministry of Education, Culture, Sports, Science and Technology of Japan.
About the Research Organization of Information and Systems (ROIS)
ROIS is a parent organization of four national institutes (National Institute of Polar Research, National Institute of Informatics, the Institute of Statistical Mathematics and National Institute of Genetics) and the Joint Support-Center for Data Science Research. It is ROIS's mission to promote integrated, cutting-edge research that goes beyond the barriers of these institutions, in addition to facilitating their research activities, as members of inter-university research institutes.
About the Institute of Statistical Mathematics
The Institute of Statistical Mathematics (ISM) is part of Japan's Research Organization of Information and Systems (ROIS). With more than 75 years of history, the institute is an internationally renowned facility for research on statistical mathematics including machine learning and evolutionary biology. ISM comprises three different departments including the Department of Statistical Modeling, the Department of Statistical Data Science, and the Department of Statistical Inference and Mathematics, as well as several key data and research centers. Through the efforts of various research departments and centers, ISM aims to continuously facilitate cutting edge research collaboration with universities, research institutions, and industries both in Japan and other countries.
Return to top of page.
|
|
Jun 10 2020 Fetal Timeline Maternal Timeline News
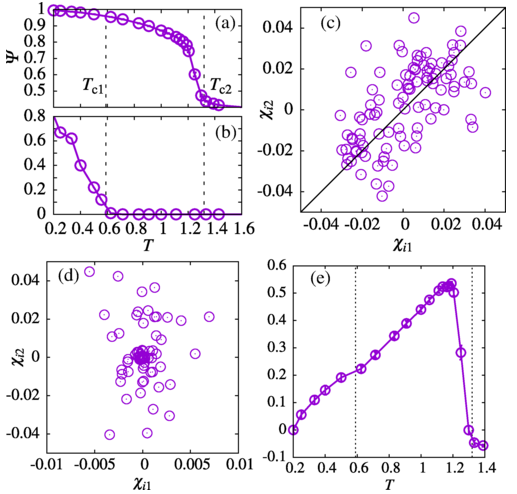 (a) T dependence of averaged fitness. (b) Fraction of matrices J(T) in which BP algorithm does not converge within 10 5 steps. For (a) and (b), vertical dashed lines indicate phase transition temperatures. (c) - (d) Scatter plots of ?i1 and ?i2 at (c) T = 1 and (d) T = 0.4. The slope of the diagonal line in (c) is 1. (e) T dependence of the averaged correlation coefficients between {?i1}?{?i,NT}. Statistical errors over J(T) is smaller than point size in the figure for all T region, and error bars are not discernible.
The model presented might be interpreted as why protein has evolved - to reduce the noise of spin.
|
|

